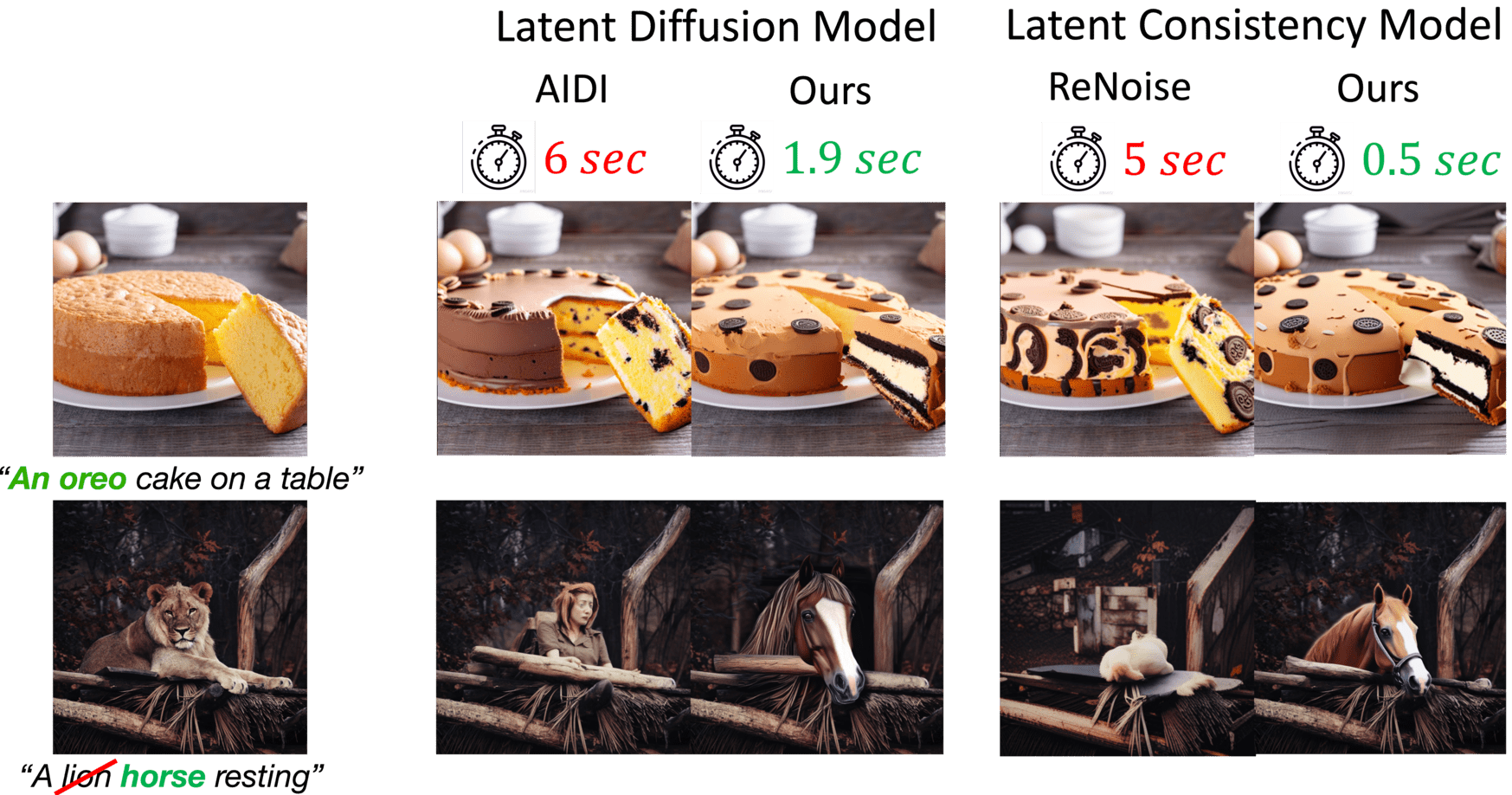

Diffusion inversion is the problem of taking an image and a text prompt that describes it and finding a noise latent that would generate the exact same image. Most current deterministic inversion techniques operate by approximately solving an implicit equation and may converge slowly or yield poor reconstructed images.
We formulate the problem by finding the roots of an implicit equation and devlop a method to solve it efficiently. Our solution is based on Newton-Raphson (NR), a well-known technique in numerical analysis. We show that a vanilla application of NR is computationally infeasible while naively transforming it to a computationally tractable alternative tends to converge to out-of-distribution solutions, resulting in poor reconstruction and editing. We therefore derive an efficient guided formulation that fastly converges and provides high-quality reconstructions and editing. We showcase our method on real image editing with three popular open-sourced diffusion models: Stable Diffusion, SDXL-Turbo, and Flux with different deterministic scheduler.
Our solution, Guided Newton-Raphson Inversion, inverts an image
within 0.4 sec (on an A100 GPU) for few-step models (SDXL-Turbo and Flux.1), opening the
door for interactive image editing.
We further show improved results in image interpolation and generation of rare objects.
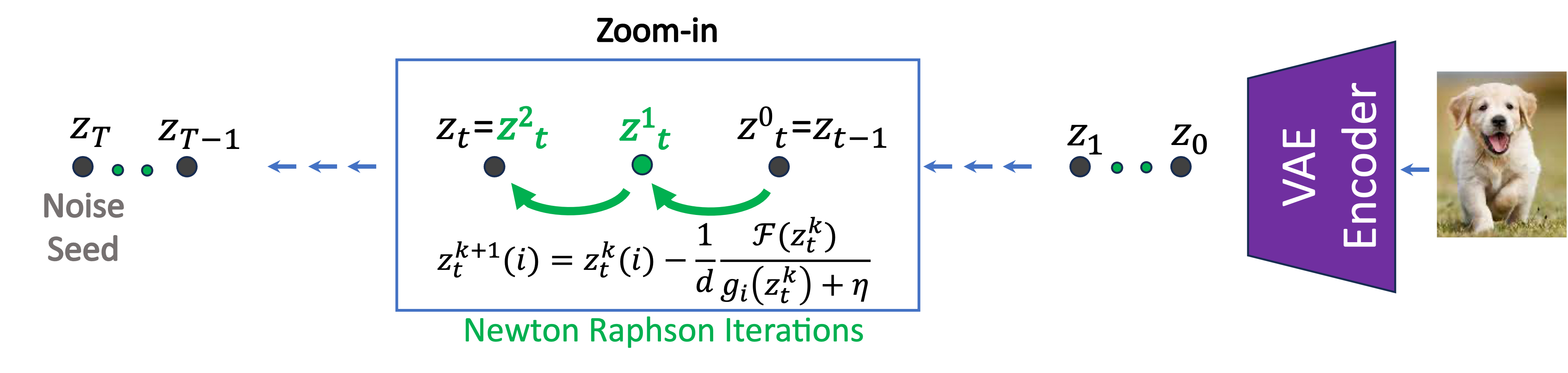 Newton-Raphson Inversion iterates over the obejective function \\(\mathcal{F}(z_t)\\). at every time
step
in
the inversion path. It starts with \(z_t^0=z_{t-1}\) and quickly converges (within 2 iterations) to
\(z_t\).
Each box denotes one inversion step; black circles correspond to intermediate latents in the denoising
process; green circles correspond to intermediate Newton-Raphson iterations.
Newton-Raphson Inversion iterates over the obejective function \\(\mathcal{F}(z_t)\\). at every time
step
in
the inversion path. It starts with \(z_t^0=z_{t-1}\) and quickly converges (within 2 iterations) to
\(z_t\).
Each box denotes one inversion step; black circles correspond to intermediate latents in the denoising
process; green circles correspond to intermediate Newton-Raphson iterations.
 (Left) Reconstruction qualitative results: Comparing image inversion-reconstruction
performance. While all baseline methods struggle to preserve the original image, GNRI successfully
excels in accurately reconstructing it. (Right) Inversion Results: Mean reconstruction quality (y-
axis, PSNR) and runtime (x-axis, seconds) on the COCO2017 validation set. Our method achieves
high PSNR while reducing inversion-reconstruction time by a factor of ×2 to ×40 on SDXL-turbo
and ×10 to ×40 on Flux.1, compared to other approaches.
(Left) Reconstruction qualitative results: Comparing image inversion-reconstruction
performance. While all baseline methods struggle to preserve the original image, GNRI successfully
excels in accurately reconstructing it. (Right) Inversion Results: Mean reconstruction quality (y-
axis, PSNR) and runtime (x-axis, seconds) on the COCO2017 validation set. Our method achieves
high PSNR while reducing inversion-reconstruction time by a factor of ×2 to ×40 on SDXL-turbo
and ×10 to ×40 on Flux.1, compared to other approaches.
@inproceedings{samuel2024lightning,
author = {Dvir Samuel and Barak Meiri and Haggai Maron and Yoad Tewel and Nir Darshan and Shai Avidan and Gal Chechik and Rami Ben-Ari},
title = {Lightning-fast Image Inversion and Editing for Text-to-Image Diffusion Models},
booktitle = {Proceedings of the International Conference on Learning Representations (ICLR)},
year = {2025}
}